How variational auto encoder can theoretically model any distribution

/ Achuth Rao MV

Similar ideas are applicable in case of Normalizing flows, You can find more details in another tutorial.

Variational Auto Encoder (VAE) is one of the famous generative models and applied for various unsupervised, semi-supervised tasks [1][2]. There is a lot of interesting ways to look at how it works [3]. But in this article, we try to develop the idea of the VAE just from the knowledge of elementary random process/probability.

First Let us look at the definition of the cumulative distribution functions (cdf) of a continues random variable X.

F_{X}(x)=\int_{-\infty}^{x}f_{x}(x)dx

where  f_{x}(x) is the probability density function (pdf). Which tell us the what the probability that the random variable takes the value in small region around the value x. Hence, if we know F_{X}(x)  or f_{X}(x) , we know all about the random variable X.

But let us ask our self what happens if random variable (X) go through a transformation y=g(x). It can be shown that the CDF of the random variable (Y) is given by

F_{Y}(y)=F_{X}(g^{-1}(y))

here we are assuming that the y=g(x) is a one to one function (invertible). But some special cases and the above derivation can be found here.

Now think about what happens if the g=F_{X}(x)…!

F_{Y}(y)=F_{X}(F^{-1}_{X}(y))=y and  f_{Y}(y)=1, y\in\{0,1\}.

y can take only value between 0 and 1 because the F_{X} function take value only between 0 and 1. Also observe that the probability is equal to 1 for the whole interval from 0 to 1.  Which is also called uniform distribution from 0 to 1 and indicated by Uni(0,1). So it is clear that the any random variable (X) can be mapped to Uni(0,1) using the function F^{-1}_{X}.

Now let us try to reverse the process, what happens if we start with random variable Y with the distribution Uni(0,1) and pass through a function x=F^{-1}_{X}(y), what is the CDF of random variable X?

It will be F_X(x)…! (Think about it)

Now we know that if we know CDF (F_X(x)) of some random variable, we can generate that random variable by first generating (sampling) the uniform random variable X from 0 to 1 and passing through y=F_X(x). This is how the computer (MATLAB) generates a random number of well-known distribution such as Gaussian/Gamma. (Want know how to generate the number uniform distribution look here). But here the assumption is that the CDF of the random variable is known. (Some cases it may not be possible to derive it analytically.)

Now we understand how we can generate random numbers from any distribution. Let us link it to VAE.

Let assume that we have a set of N-identical and independent samples\{x_i\}_{i=1}^{N} from a unknown and arbitrary probability distributionf_{X}(x) . Our goal is to findf_{X}(x) . We saw before that we can map from any distributionf_{X}(x)  to Uni(0,1) and vice-versa. But the function that should be used is known because thef_{X}(x)  or the F_X(x) is known. Hence we propose the following. Let us map x to y using a function (f) (Using deep neural network/any other model) and try to optimize function (f) the distribution of y close to Uni(0,1).  We already saw in the previous post the shallow neural network can approximate any function given enough number of hidden units. So the function (f) can be approximated by either a shallow/deep network. At the end of the training, we get the neural network mapping f=F^{-1}_X(x).

But there are two main questions:

  1. How do we make the distribution of y close to Uni(0,1)?
  2. What is the use of approximating F^{-1}_X(x), we cannot generate the data from the generative models?

The first question is difficult in terms of learning/objective function of the neural network (issues like differentiability/backpropagation) and the second question is not answered by our solution.

So let us propose some other modification to this. Let us map from x to y and then map y to x_{recon}. Now our objective is two-fold:

  1. Make the x_{recon} as close as possible to x.
  2. To make the generative process clear, we need to force the distribution of y to Uni(0,1).

The first objective is simple, we can use error like mean squared error or weighted mean squared error make the x_{recon} as close as possible to x. The second one is slightly challenging. But the second objective will allow us to generate data (The whole purpose of the generative model).

But we can look the second objective in a slightly different way, Let us ask our self, can we generate the numbers from arbitrary distribution given the random number from a Gaussian distribution (z)?

The answer is simple, Let us the function g(z) map from Gaussian distribution to uniform distribution (u) and another function h(u) map from a uniform distribution to required distribution (x). The outline is given below.

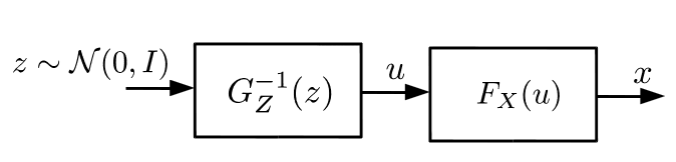
Screenshot from 2017-09-17 12:27:02

Generating data from the arbitrary distribution using the Gaussian distributed data. Where the distribution of u is a uniform distribution.

Here we assumed that simplest Gaussian distribution of zero mean and identity co covariance matrix. The overall function to generate a random variable from the distribution p(x) can be written as h(g(z)), where the distribution of z is Gaussian.

So now our whole process can be written as shown in the figure.

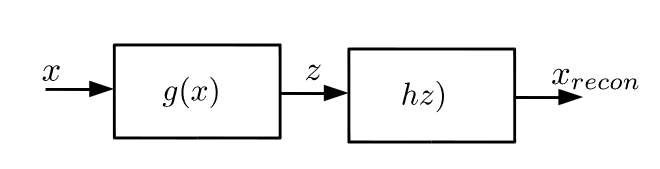
Screenshot from 2017-09-17 12:54:23

Our whole process block diagram

start with the data x and map it to a variable y  using a function G(x) and map the y to x_{recon} using the function H(z).  The functions G and H are approximated using neural networks. The first goal is measure the closeness of the x and  x_{recon}  using E(x, x_{recon} ), where E is any error function and make the distribution of z close to Gaussian distribution of zero mean and identity co covariance matrix (\mathcal{N}(0,I)). The closeness of the two distribution p(x) and p(y) is measured using the KL divergence.(KL(p(x)||p(y)).

So the overall objective sum of both the objectives:

E(x, [latex]x_{recon} )+(KL(p(z)||\mathcal{N}(0,I))[/latex]

We can see that the objective is exactly same as the VAE objective…!

The specific details of the implementation and the optimization can be found in the main paper  [1]. Once the network is learned the data generated from the model is easy.  First sample from the \mathcal{N}(0,I) and then pass it through h(z) to get the samples of the data.

In summary:

  1. Generating random numbers from the arbitrary distribution from Gaussian/Uniform distribution and the reverse process is known for a long time.
  2. Use neural network (theoretically approximate any function) to approximate the required function to map from one distribution to another.
  3. We saw the VAE is about reconstructing the data and forcing a distribution in a particular layer of a neural network can help in generating the data.
  4. The second term of the objective can be evaluated in closed form for Gaussian distribution and it allows for the backpropagation.
  5. There are some intricate details related to the learning process (finite sample size) is not discussed here.

Notes:

  1.  Last two points in the summary are the main contribution of [1].
  2. The [1] approaches the problem from the Variational method framework. Where the true likelihood is lower bounded by the objective we just found above.

 

Have a great day.

-Achuth

Reference:

[1] Auto-Encoding Variational Bayes

[2]Tutorial on Variational Autoencoders

[3] Other nice blogs about VAE:

 

 

 

Leave a comment